Curriculum Temperature for
Knowledge Distillation

中文解读

李政 南开大学/旷视科技


知乎链接

一句话概括:

相对于静态温度超参蒸馏，本文提出了简单且高效的动态温度超参蒸馏新方法。

背景问题：

目前已有的蒸馏方法中，都会采用带有温度超参的KL Divergence Loss进行计算，从而在教师模型和学生模型之间进行蒸馏，公式如下：
Lkd(qt,qs,τ)=∑i=1Iτ2KL(σ(qit/τ),σ(qis/τ))

其中，温度超参的大小控制了两个预测结果和的平滑程度，决定了两个概率分布间的距离，τ越大(τ > 1)，就会使得概率分布越平滑(soft)， τ越小(0 < τ < 1)，越接近0，会使得概率分布越尖锐(sharp)。

τ的大小影响着蒸馏中学生模型学习的难度，不同的τ会产生不同的蒸馏结果。 而现有工作普遍的方式都是采用固定的温度超参，一般会设定成4。

那么这就带来了两个问题：

1.不同的教师学生模型在KD过程中最优超参不一定是4。如果要找到这个最佳超参，需要进行暴力搜索，会带来大量的计算，整个过程非常低效。

2.一直保持静态固定的温度超参对学生模型来说不是最优的。基于课程学习的思想，人类在学习过程中都是由简单到困难的学习知识。那么在蒸馏的过程中，我们也会希望模型一开始蒸馏是让学生容易学习的，然后难度再增加。难度是一直动态变化的。

于是一个自然而然的想法就冒了出来：

在蒸馏任务里，能不能让网络自己学习一个适合的动态温度超参进行蒸馏，并且参考课程学习，形成一个蒸馏难度由易到难的情况？

于是我们就提出了CTKD来实现这个想法。

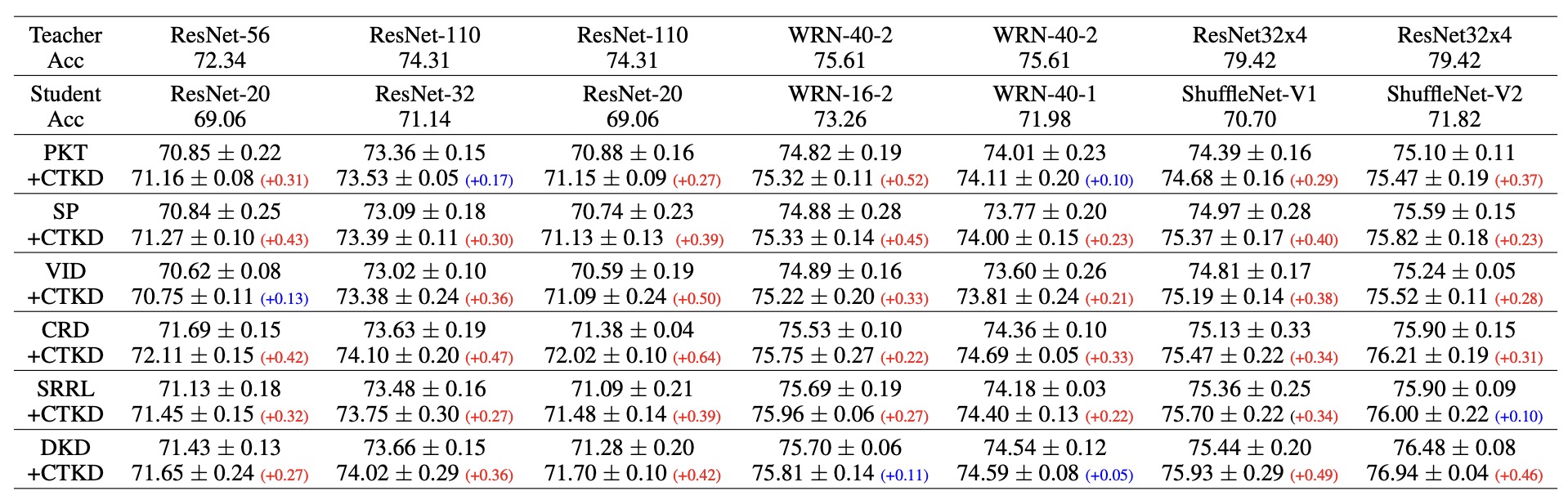
方法：

既然温度超参τ可以在蒸馏里决定两个分布之间的KL散度，进而影响模型的学习，那我们就可以通过让网络自动学习一个合适的τ来达到以上的目的。

于是以上具体问题就直接可以转化成以下的核心思想：

在蒸馏过程里，学生网络被训练去最小化KL loss的情况下，τ作为一个可学习的参数，要被训练去最大化KL-loss，从而发挥对抗(Adversarial)的作用，增加训练的难度。随着训练的进行，对抗的作用要不断增加，达到课程学习的效果。

以上的实现可以直接利用一个非常简单的操作：利用梯度反向层GRL(Gradient Reversal Layer)来去反向可学习超参τ的梯度，就可以非常直接达到对抗的效果，同时随着训练的进行，不断增加反向梯度的权重λ，进而增加学习的难度。

CTKD的论文的结构图如下：

图挂了= =
图1. CTKD结构图。(a)对抗温度超参的训练流程，(b)由易到难的课程训练方法。

CTKD方法可以简单分为左右两个部分：

1. 对抗温度超参τ的学习部分。

这里只包含两个小模块，一个是梯度反向层GRL，用于反向经过温度超参τ的梯度，另一个是可学习超参温度τ。

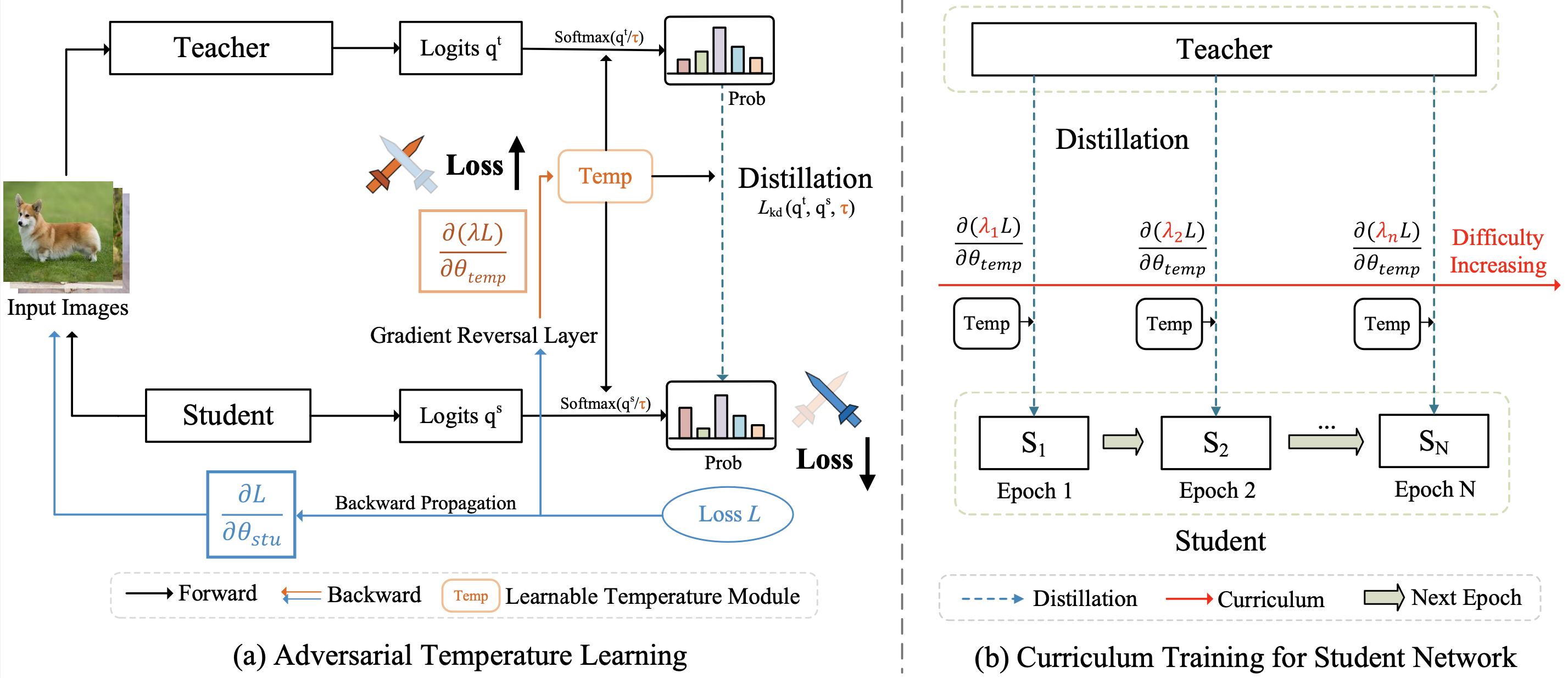
其中对于温度超参τ，有两种实现方式:

图挂了= =
图2. 两种不同的可学习温度模块。(a)全局温度法，(b)实例级温度法。

第一种是全局方案(Global Temperature)，对于全局只会产生一个τ，代码实现非常简单，就一句话：

self.global_T = nn.Parameter(torch.ones(1), requires_grad=True)

第二种是实例级别方案(Instance-wise Temperature)，即对每个单独的样本都产生一个τ，也就是对于一个batch中，如果有128个样本，那么就instance-wise CTKD就会生成对应128个τ。代码实现也很简单，就是两层1x1 conv组成的MLP，将教师和学生的输出concat在一起，送入MLP里面，最后输出128个温度值。

Instance-wise Temp的代码实现已经训练log都已经在GitHub里面提供，在这里。

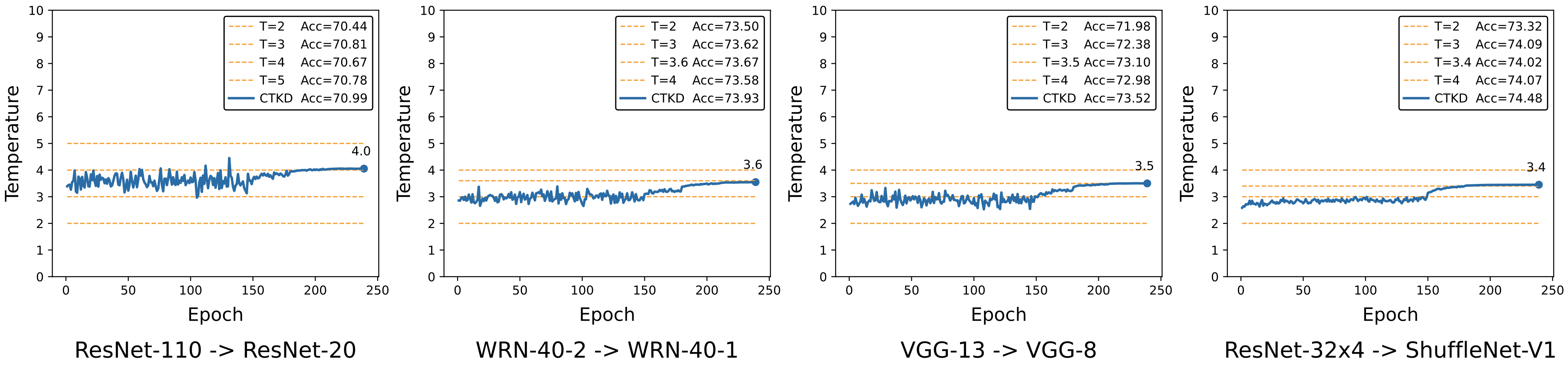
2. 难度逐渐增加的课程学习部分。

随着训练的进行，不断增加GRL的权重λ，达到增加学习难度的效果，参考图1.(b)中所画。

在论文的实现里，我们直接采用Cosine的方式，让反向权重λ从0增加到1。

以上就是CTKD的全部实现，非常的简单有效。

总结一下方法：CTKD总共包含两个模块，梯度反向层GRL和温度预测模块，

CTKD方法可以作为即插即用的插件应用在现有的SOTA的蒸馏方法中，取得广泛的提升。

实验结果：

我们在三个数据集：CIFAR-100，ImageNet和MS-COCO上验证了CTKD方法的性能。在CIFAR 100数据集上, CTKD的实验结果如下所示：

图挂啦
表1. 在CIFAR-100上的准确率。

作为一个即插即用的插件，应用在已有的SOTA方法上:

图挂啦
表2. CTKD作为插件应用在不同的方法上。

在ImageNet上的实验：

图挂啦
表3. 在ImageNet上的准确率。

温度超参的整体学习过程可视化：

Temperature Curve
图3. 温度参数值在训练中的变化过程。

由以上图可以看到，CTKD整体的动态学习τ的过程。随着训练的进行，最后收敛并且稳定下来。对于不同的teacher-student pair有不同的最终收敛值。

将CTKD应用在多种现有的蒸馏方案上，可以取得广泛的提升效果。

问题反馈与解答：

1. 问：代码实现的λ与论文中公式11表述不一致。

答：论文里面表述写的是对反向梯度层的lambda从0按照cos的方式增加到1，

在实现的代码中，scripts/run_cifar_distill.sh里面的超参设定是--decay_max 0 --decay_min -1.

这里表达的意思是，对梯度相乘的超参从0下降到-1，达到反向梯度效果.

论文里面的公式11比代码实现公式多了一个π。以前学过三角函数的公式cos(π+x)=-cosx。

所以在这里，两个的效果是等价的。

2. 问：把GRL用在别的方法上去学习超参不work，第一轮之后直接max。

答：在应用GRL的时候，需要考虑方法本身是否存在约束，GRL发挥的是adversarial对抗的作用，没有约束就会直接朝着反向最大化优化下去。

在KD loss的优化中是存在约束的，在KD loss里面T^2* KLD 这里，T^2的最大化会让KLD loss里面的T变大，使教师和学生的分布都变平滑，从而使KLD loss整体减小。也就是说，T变大，KLD loss就会变小，反之亦然，从而整体的KD loss能够保持在一个合理范围。这两个是存在动态约束的。

如果要学习的超参没有约束，没有对抗的效果在里面。在反向最大化整体的loss的时候，就可能会让超参直接学习到设置的范围上界。

所以直接应用GRL需谨慎，要根据具体任务来。

另外的一个可能存在的原因是，GRL的对抗幅度过强，一次优化就会产生很大的梯度，学习温度模块没办法学会，这时候可以尝试去降低GRL的权重λ，改成一个很小的值，让温度模块慢慢训。

3. 问：CTKD工作历程以及motivation。

答：一开始的工作启发是来自于< Meta Knowledge Distillation >这篇工作。这篇工作的方式是一个温度参数模块预测的温度超参T，方式是在额外划分的验证集上最小化KL loss。

MKD工作存在的问题是，1. 需要额外划分验证集，不是那种拿到code就可以直接训练的方法。2.方法应用的条件下是heavy aug，而普通的蒸馏训练是不用heavy aug的，MKD难以作为插件集成进现有主流的kd方法里。3.没开源代码，不易复现。

CTKD工作受到MKD工作的启发，也在思考可不可以有另外一种方式去学习。第一种非常直觉性的探索方式就是，给定单个可学习的超参T，探索直接最小化KL loss的方向的，也就是没有GRL的情况。

这一部分的实验下来，发现T无法收敛，会保持在范围的上边界。比如范围是[1,21]的话，就会在20.0+的这种状态，显然是无效的。

于是我们直接对一些model pair不同T下acc和total KL loss的统计，发现对应acc更好的T所有样本的KL loss加在一起不是想象中的是acc最好的时候KL loss就是最低。而是KL loss相对更大时候，acc反而会更好。

这样的方式也就好理解了，KL loss越大，侧面反应蒸馏难度高的时候kd效果往往会更好。

于是，CTKD就走了一个与MKD相反的方向。MKD在最小化KD loss，CTKD的目标是最大化KD loss。要达到对抗效果的非常简单的方法就是GRL。于是就有了GRL这种反向思路出现。

以上为全部内容解读